A Different BMI Formula

Should there be a different BMI formula? Many have suggested that it would be better to come up with a formula different than either the body mass index which is based on the scaling of weight to the power of two or the formula known as the Ponderal Index which is based on the weight being a factor based on the power of three. The cube root (power of three) is the most natural of relationships for objects that increase in size. For example if you double the side of a 1 inch cube to make it a 2 inch cube it will have a volume of 2*2*2 or 2³ or 8 cubic inches. If that cube was of uniform weight it would have 8 times as much weight. If you double a person’s height would you not expect you would double their weight?

Here are some pictures to represent the problem. Think of one brick as some one 5 feet tall and 120 pounds. How much would this person weigh if they were 10 feet tall?

If all proportions were exactly the same this person would weigh eight times as much or be 960 pounds.














But taller people do not have the same proportions as shorter people. Are they simply stretched? If so they would be 240 pounds.



















Would they be squared as the BMI formula suggests? If so they would weigh about 480 pounds.

The BMI formula was first observed using some data that was observed on men hundreds of years ago. Let us look at some more recent data which was taken from the 1960 census a time when obesity was not such a big problem. I will try to show the comparison in a visual form. I will also try to show whether a different number between a square (2) and a cube (3) would be more appropriate to use an exponent. It has been suggested that a number between 2.3 and 2.7 would be better.¹ Of course I realize that this analysis was looking at all of the people in 1960 and to make a decision requires looking only at the weight of healthy people, and I do not know where that data is.

Why do I use the 1960 data? Because as the chart below indicates, there were fewer overweight people in 1960.

Table 2. Age-adjusted* prevalence of overweight, obesity and extreme obesity among U.S. adults, age 20-74 years**

	NHES I 1960-62 n=6,126	NHANES I 1971-74 n=12,911	NHANES II 1976-80 n=11,765	NHANES III 1988-94 n=14,468	NHANES 1999-2000 n=3,603	NHANES 2001-02 n=3,916	NHANES 2003-04 n=3,756	NHANES 2005-06 n=3,835
Overweight (BMI greater than or equal to 25.0 and less than 30.0)	31.5	32.3	32.1	32.7	33.6	34.4	33.4	32.2
Obese (BMI greater than or equal to 30.0)	13.4	14.5	15.0	23.2	30.9	31.3	32.9	35.1
Extremely obese (BMI greater than or equal to 40.0)	0.9	1.3	1.4	3.0	5.0	5.4	5.1	6.2

*Age-adjusted by the direct method to the year 2000 U.S. Bureau of the Census estimates using the age groups 20-39, 40-59, and 60-74 years.

**NHES: National Health Examination Survey; NHES included adults 18-79 years, NHANES I & II did not include individuals over 74 years of age, thus trend estimates are based on age 20-74 years. Pregnant females were excluded from analyses.

Source:
http://www.cdc.gov/nchs/data/hestat/overweight/overweight_adult.htm

If you look at the next chart, you can see that the BMI formula (power of 2) gives a better fit than the Ponderal Index (power of 3). For the power of 3 to be a better fit it would have to give more similar numbers irrespective of a person’s height.

You can also see that the number that gives the most consistent results irrespective of a persons height is the BMI formula to the power of 1.8 rather than to the power of two.

BMI of Ave Men (1960 25-34 yrs) (Smoothed average Table 5 NCHS "Weight by Height and Age of Adults")
height	weight	BMI (power 2)	power 2.5	power 3 (PI)	power 2.2	power 1.8	power 2.1	power 1.9	power  1.85	power 1.75
74	194	24.90787043	18.16786	13.251687	21.9545	28.25854	23.38461	26.53036	27.38081767	29.164394
73	190	25.06722089	18.4089	13.519157	22.15516	28.36204	23.56625	26.66379	27.49980882	29.2513108
72	186	25.22587612	18.65362	13.793677	22.35697	28.46292	23.74814	26.79556	27.61666238	29.3351161
71	181	25.24411702	18.79811	13.998069	22.43581	28.40394	23.79858	26.77746	27.57871295	29.2538615
70	177	25.39659502	19.04626	14.283799	22.63545	28.49455	23.97631	26.90102	27.68632146	29.3263783
69	172	25.39969916	19.18612	14.492582	22.70346	28.41614	24.01377	26.86562	27.63000693	29.224647
68	168	25.54405047	19.43652	14.789284	22.89925	28.49432	24.18552	26.97889	27.72625148	29.2836644
67	163	25.52914713	19.5696	15.001262	22.9538	28.39344	24.20725	26.92323	27.64856427	29.158383
66	159	25.66300807	19.82069	15.308404	23.14366	28.45661	24.3708	27.02373	27.73091556	29.2012857
65	154	25.62667817	19.9443	15.521913	23.18157	28.32968	24.37348	26.94431	27.62831353	29.0488593
64	150	25.74717699	20.19402	15.838569	23.36291	28.37477	24.52609	27.02906	27.69374392	29.0725443
63	145	25.6853336	20.30477	16.051327	23.38031	28.2176	24.50574	26.92171	27.56203949	28.8887518
62	141	25.78897261	20.55045	16.37603	23.54989	28.24094	24.64402	26.98712	27.60691334	28.8895244
hi - low		0.881102189	2.382586	3.1243436	1.595396	0.276953	1.259411	0.498703	0.35009789	0.44636437
62 -74		0.881102189	2.382586	3.1243436	1.595396	-0.0176	1.259411	0.456763	0.226095667	-0.27486959
ave BMI		25.44813428

Therefore, this data suggests that if we must change the BMI formula it should be to the power of 1.8 rather than the 2.2 or 2.3 that has been suggested. The real kicker is that no one has a good set of data for healthy people just data for average people. When we get better data, then perhaps the formula can be changed. Perhaps we should start keeping records of those people who live to be at least 90 and then go back in time to see how tall and how much they weighed when they were young.

We all know that the shape of women are different. It looks like a power of about 1.9 would describe how the weight increases with an increase of height. See the table below.

BMI of Ave Women (1960 25-34 yrs) (Smoothed average Table 5 NCHS "Weight by Height and Age of Adults")
height	weight	BMI (power 2)	power 2.5	power 3 (PI)	power 1.50	power 1.8	power 2.1	power 1.9	power  1.70	power 1.60	power 1.4
68	156	23.71947544	18.04819	13.732906	31.17284	26.45901	22.45799	25.05182	27.94524163	29.5149554	32.92385
67	152	23.80632125	18.24896	13.988907	31.05607	26.47732	22.57363	25.10632	27.92317806	29.4479928	32.75197
66	148	23.88757984	18.44945	14.249332	30.92865	26.48791	22.68477	25.15417	27.89237191	29.3713029	32.56857
65	144	23.96260816	18.64921	14.513996	30.78985	26.49009	22.79079	25.19468	27.85211682	29.2841697	32.37295
64	140	24.03069852	18.84775	14.782664	30.63891	26.48312	22.89101	25.22713	27.80164556	29.1858181	32.16434
63	136	24.09107151	19.04447	15.055038	30.47497	26.46616	22.98469	25.25071	27.74012391	29.0754084	31.94189
62	132	24.14286798	19.23872	15.330752	30.29714	26.43833	23.07099	25.26454	27.66664397	28.9520301	31.70473
61	128	24.18514007	19.42973	15.609359	30.10443	26.39863	23.149	25.26766	27.58021659	28.814695	31.45189
60	124	24.21684108	19.61666	15.890316	29.89579	26.34599	23.21769	25.25899	27.47976294	28.6623291	31.18232
59	120	24.23681401	19.79852	16.172971	29.67006	26.27923	23.27593	25.23737	27.36410502	28.4937639	30.89491
58	116	24.24377861	19.9742	16.456543	29.426	26.19707	23.32245	25.20151	27.23195511	28.3077267	30.58844
57	112	24.23631669	20.14245	16.7401	29.16224	26.09807	23.35585	25.14997	27.08190375	28.1028294	30.26159
hi - low		0.524303171	2.094257	3.0071938	2.0106	0.392028	0.897868	0.215833	0.863337872	1.41212601	2.662262
68-57		0.51684125	2.094257	3.0071938	-2.0106	-0.36094	0.897868	0.098147	-0.863337872	-1.41212601	-2.66226

More Appropriate Exponent for BMI

Nick Korevaar has suggested that an exponent of between 2.3 and 2.7 would be more accurate than the present exponent of 2.0¹

. The proplem is that his analysis only looked at the BMI of growing children and not adults. I am looking for a better exponent for adults. So far I have only given a visual explaination and a look at the data. I will now use the same math as explained by Korevaar, but using exel to find the best exponent for adults. I will start with the last example of data, women 25 to 34.

BMI of Ave Women (1960 25-34 yrs) (Smoothed average Table 5 NCHS "Weight by Height and Age of Adults")
height	weight	ht m	wt kg	ln ht(m)	Ln wt(kg)
68	156	1.72720	70.76041	0.54650	4.25930
67	152	1.70180	68.94604	0.53169	4.23332
66	148	1.67640	67.13167	0.51665	4.20666
65	144	1.65100	65.31730	0.50138	4.17926
64	140	1.62560	63.50293	0.48588	4.15109
63	136	1.60020	61.68856	0.47013	4.12210
62	132	1.57480	59.87419	0.45413	4.09225
61	128	1.54940	58.05982	0.43787	4.06147
60	124	1.52400	56.24545	0.42134	4.02973
59	120	1.49860	54.43108	0.40453	3.99694
58	116	1.47320	52.61671	0.38744	3.96303
57	112	1.44780	50.80235	0.37005	3.92794

This chart shows what we saw by exploring the data. For this category, which is women 25 to 34, an exponent of lower than 2.0 would be better. In this case 1.62 would be better.

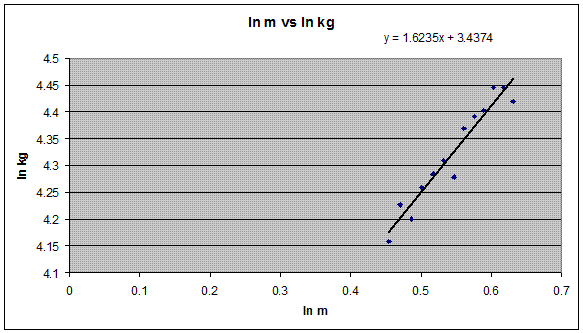
I have run this test on other age groups and for both men and women. I get results for and exponent of from 1.1 to 1.8. None of these seem to be of tremendous advantage over 2.0 which never seems to be off by more than about a half a BMI value.

Summary:
It has been shown that for adults an exponent of less than 2.0 seems to be slightly better. Others have show that for children and young people, a BMI exponent of greater than 2.0 would be best. The problem with both studies is that the data includes a variety of body types and not only healthy people but also people who are over weight and underweight. Also there would have to be a seperate exponent for each age group. In conclusion, until there is much better data, It would be best to just keep the exponent at 2.0. Even though it is not a perfectly reliable indicator of obesity, it gives the medical professional a starting point for discussion, and as it does combine height and weight into one number.